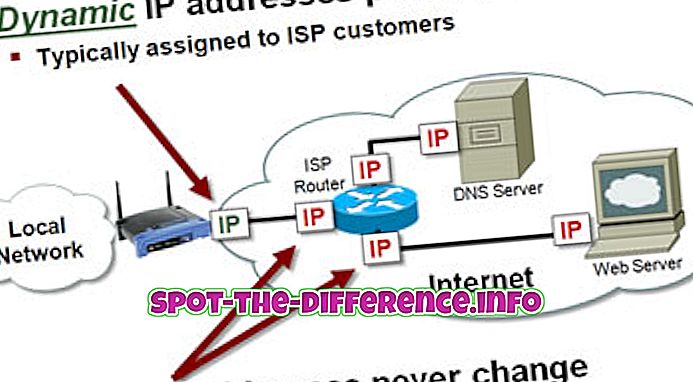
Ключова різниця: парабола - це конічна секція, яка створюється, коли площина розрізає конічну поверхню, паралельну стороні конуса. Гіпербола створюється, коли площина розсікає конічну поверхню, паралельну осі.

Парабола і гіпербола є двома різними словами, розділами і рівняннями, які використовуються в математиці для опису двох різних розділів конуса. Вони відрізняються за формою, розміром і різними іншими факторами, включаючи формули, які використовуються для його розрахунку. Щоб їх зрозуміти, давайте спочатку зрозуміємо конус і різні конічні перерізи.

Конічний розріз - це крива, яка виходить, коли площину перетинає конус різними способами. Розрізи, які виходять з перетину, включають еліпс, коло, параболу і гіперболу. Згідно з аналітичною геометрією, конічний визначається як «плоска алгебраїчна крива ступеня 2.» Популярне визначення конічного перерізу включає точку фокусування, пряму пряму і ексцентриситет. Очікується, що точка фокусування і лінії directrix знаходяться в фіксованому раціоні в конічному. Співвідношення відоме як ексцентриситет конічного перетину. Ексцентричність еліпсів, параболей і гіперболів відрізняються; еліпси мають ексцентриситет менше 1, параболи мають ексцентриситет, що дорівнює 1, а гіперболи мають ексцентриситет більше 1. Найбільш ранні відомі роботи з конічних перетинів можуть дати початок IV століття до н.е. вирішити проблему подвоєння куба шляхом використання параболи.

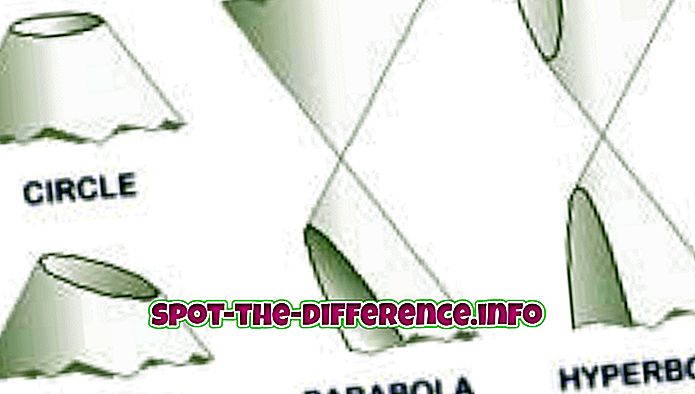
Парабола - це конічний розділ, який створюється, коли площина перетинається з конусом. Parabolae або parabolas утворюють 'з перетину правої кругової конічної поверхні і площини, паралельної генеруючій прямій поверхні.' Інший спосіб створення параболи полягає в тому, що локус точок на площині, рівновіддалені від фокуса, і directrix створюють параболу. В алгебрі параболи зазвичай використовуються у графіках квадратичних функцій, використовуючи формулу y = x ^ 2.

Лінія, що розділяє параболу через середину, відома як вісь симетрії; ця лінія також перпендикулярна прямій і проходить через фокус. Точки, що знаходяться на осі симетрії, що перетинають параболу, називаються вершиною. Відстань між вершиною і фокусом відома як "фокусна відстань". Parabolas може відкриватися в будь-якому напрямку, включаючи вгору, вниз, вправо або вліво. Також головною особливістю параболів є те, що вони однакові, лише відрізняються за розміром. Їх можна змінити і змінити точно, щоб відповідати будь-якій іншій параболі. Параболи використовуються в різних областях застосування, таких як автомобільні відбивачі фар, проектування балістичних ракет тощо. Вони також відіграють важливу роль у фізиці, техніці, математиці тощо.

Гіперболи являють собою гладку криву, яка виникає, коли площина перетинається з конусом, паралельним осі у, що створює розріз уздовж сторони конуса. Гіпербола визначається її геометричними властивостями або рівняннями, для яких вона є набором рішень. Термін «гіпербола» походить від грецького слова, що означає «надмірне» або «надмірне». Вважається, що цей термін придуманий Аполлонієм Пергом, який багато в чому сприяв вивченню конічних перетинів.

Як відомо, гіпербола має гілки, які є дзеркальними зображеннями один до одного і нагадують два нескінченних лука. Точки на двох гілках, найближчі один до одного, називаються вершинами. Лінія, що з'єднує вершини, відома як поперечна вісь або велика вісь, що відповідає основному діаметру еліпса. Середина поперечної осі відома як центр гіперболи. Рівняння гіперболи записується як x2 / a2- y2 / b2 = 1. Гіперболи використовуються в різних додатках у сучасному світі, включаючи шлях, за яким слідує тінь кінчика сонячного годинника, форма відкритої орбіти; використовується як арка у багатьох побудованих будівлях, як рівняння з математики та геометрії, фізики тощо.

Гіперболи і параболи - це відкриті криві, що означає, що вони не закінчуються і тривають нескінченно до нескінченності, що еліпси і кола не можуть зробити.